CALCULO DIFERENCIAL

PARA TODO

El Calculo Diferencial e Integral es la herramienta intelectual mas poderosa creada por el hombre, con el podemos comprender TODO fenomeno natural, y comprender significa usualmente manipular, desde la fabricacion de un simple tornillo, con el perfecto equilibrio de materiales y flujo de calor para hacer metal resistente, hasta el calculo de velocidad de bombeo de la sangre en un corazon artifical, donde sea que veamos, el calculo esta presente.

Vivimos en una sociedad tecnologica, y tecnologia solo significa una cosa: Matematicas, y la herramienta mas util de ellas es el Calculo, aqui unos cuantos ejemplos para dejar bien claras las cosas:

Twitter, el Calculo Diferencial nos permite entender la Teoria electromagnetica que se uso para diseñar los circuitos de los telefonos inteligentes y las computadoras. (Vease Leyes de Gauss)
Facebook, las pantallas de las computadoras, las tablets o los telefonos son diseños basados en las teorias de Estado Solido, de Luminosidad y de transductores dactiles, todas ellas, Teorias Fisicas desarrolladas con mucho Calculo Diferencial.
Aviones, desde la reservacion de boletos, hecha con una computadora desarrollada siguiendo los principios de la matematica cibernetica, hasta el uso eficiente del flujo de combustible en el motor, (Ecuaciones lagrangianas), todo en ellos es calculo.
Futbol, no seria el negocio multimillonario que es sin los Estadios, en los que el calculo de resistencia de Materiales, resistencia estructural y distribucion, todo ello imposible sin las ecuaciones diferenciales o las integrales.
Conciertos, donde sea que haya electronica hay Calculo, en los microfonos, en los baffles, en las pantallas gigantes, en la reservacion de boletos, en los instrumentos musicales (una buena guitarra no lo seria si no se diseñara usando las leyes de la acustica, las cuales, por supuesto que estan basadas en el Calculo Diferencial)
Automoviles, un buen motor, es una obra maestra de la ingenieria, la cual como te imaginaras, es puro Calculo, las lineas aerodinamicas de la carroceria, estan basadas en estudios sobre Aerodinamica, leyes, que solo se pueden expresar por medio del calculo.
Dios, no es posible entender la grandeza de sus creaciones sin el Calculo, el cual nos permite entender todo el universo y que ha sido llamado, "El Calculo es el verdadero lenguaje de Dios"
Amor, para hacer feliz a nuestra pareja y a nuestros hijos es necesario ganar dinero, la economia de un pais avanzado, se basa en complejas ecuaciones matematicas, planeaciones, prestamos, y demas actividades, requieren de un calculo realmente avanzado y de muy buenas computadoras.
Contaduria, los mejores contadores del mundo, tienen que ver como es el flujo de dinero, de produccion, de ventas, y donde sea que este la palabra flujo, estan las ecuaciones Eulerianas, que describen el flujo como una serie de integrales y derivadas.
Biologia, desde las ecuaciones de Depredador-presa hasta la adaptacion de un Ecosistema estable son ecuaciones diferenciales o integrales.
Medicina, cada vez se esta haciendo mas tecnologica, un Tomografo o la velocidad de disolucion de un medicamento en la sangre se hacen con Calculo.
Abogacia, y si creias que aqui estarias a salvo del Calculo, te equivocas, los mejores abogados del mundo tienen que hacer complejos calculos para la evalucion de un riesgo de fusion de compañias enormes, ver los porcentajes de indeminizacion en contratos multimillonarios, y no lo pueden dejar a cargo de segundones, un solo contrato de un grupo musical o de una empresa trasnacional requiere de complejos calculos financieros.

Antiderivadas

La antiderivada es la función que resulta del proceso inverso de la derivación, es decir, consiste en encontrar una función que, al ser derivada produce la función dada.

Por ejemplo:

Si f(x) = 3×2, entonces, F(x) = x3, es una antiderivada de f(x). Observe que no existe una derivada única para cada función. Por ejemplo, si G(x) = x3+ 5, entonces es otra antiderivada de f(x).

La antiderivada también se conoce como la primitiva o la integral indefinida se expresa de la siguiente manera: en donde: f(x) es el integrando; dx, la variable de integración o diferencial de x y C es la constante de integración.

Notación

Teorema

Si dos funciones h y g son antiderivadas de una misma función f en un conjunto D de números reales, entonces esas dos funciones h y g solo difieren en una constante.

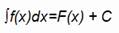
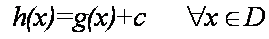
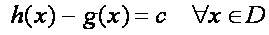
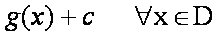Conclusión: Si g(x) es una antiderivada de f en un conjunto D de números reales, entonces cualquier antiderivada de f es en ese conjunto D se puede escribir como Monografias.com